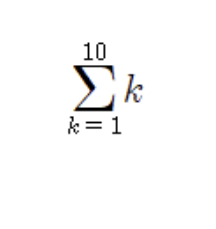시그마( ∑ )
- 1+2+3+4+ … + 10
- 따라서 1부터 10까지의 합은
참고 블로그 https://calcproject.tistory.com/663
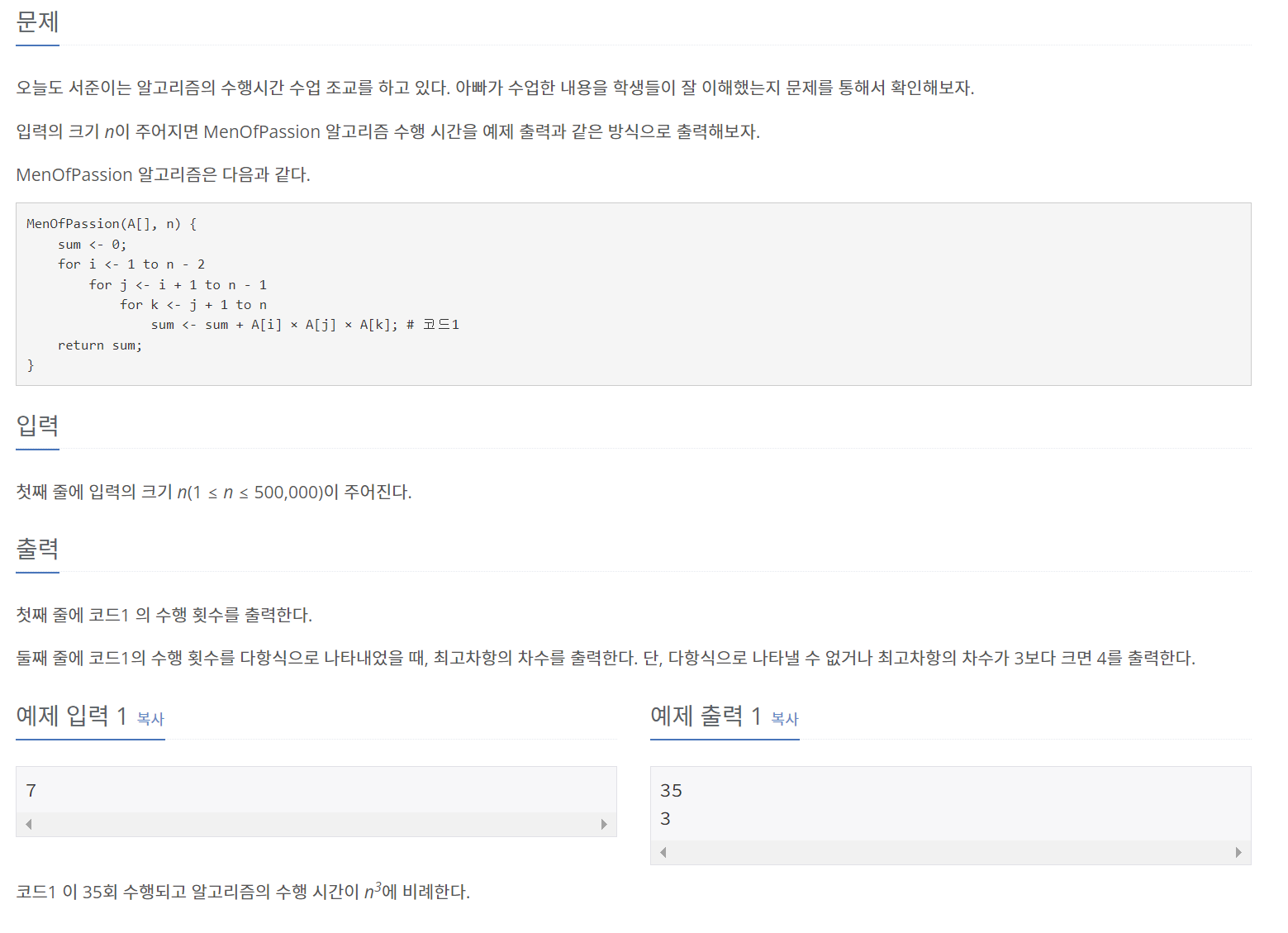
백준 24267 문제
n이 1, 2일 때, 시행 X
n이 3일 때, 시행횟수 : 1번
n이 4일 때, 시행횟수 : 4번
n이 5일 때, 시행횟수 : 10번
n이 6일 때, 시행횟수 : 20번
n이 7일 때, 시행횟수 : 35번
수열로 나열하면
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| an | 1 | 4 | 10 | 20 | 25 | 46 | 74 | |||||||
| bn | 3 | 6 | 10 | 15 | 21 | 28 | ||||||||
| cn | 3 | 4 | 5 | 6 | 7 |
cn = n + 2가 된다.
여기서 n은 입력받은 n이 아니고 cn 기준의 n이다
그렇다면 bn = 3 + cn 즉, bn = 3 + ∑(n + 2)가 되기 때문에
bn = 3 + ∑n + ∑2 가 되고, 이때의 ∑의 k=1, n은 bn 기준의 n이기 때문에, n = n-1이 된다. 왜냐하면 첫번째 n은 3이기 때문에
이걸 풀어보면
bn = 3 + (n-1)n½ + 2n-2
bn = (n²-n)*½ + 2n+1
bn = (n²-n)½ + (4n+2)½
bn = (n² + 3n + 2) * ½
이 된다
그렇다면
an = 1 + ∑bn이 되고, ∑는 k=1, n=n-1이 된다. 위와 같은 이유로…
an = 1 + ∑((n² + 3n + 2) * ½)
an = 1 + ½∑n² + 3/2∑n + ∑1
an = 1 + ½ * (n-1) * n * (2n-1) * 1/6 + 3/2 * (n-1) * n * 1/2 + n-1
an = 1/12 * ( 2n³ - 3n² + n ) + 3/4 * (n² - n) + n
an = 1/12 * ( 2n³ - 3n² + n ) + 9/12 * (n² - n) + n
an = 1/12 * ( 2n³ - 3n² + n + 9n² - 9n + 12n )
an = 1/12 * ( 2n³ + 6n² + 4n )
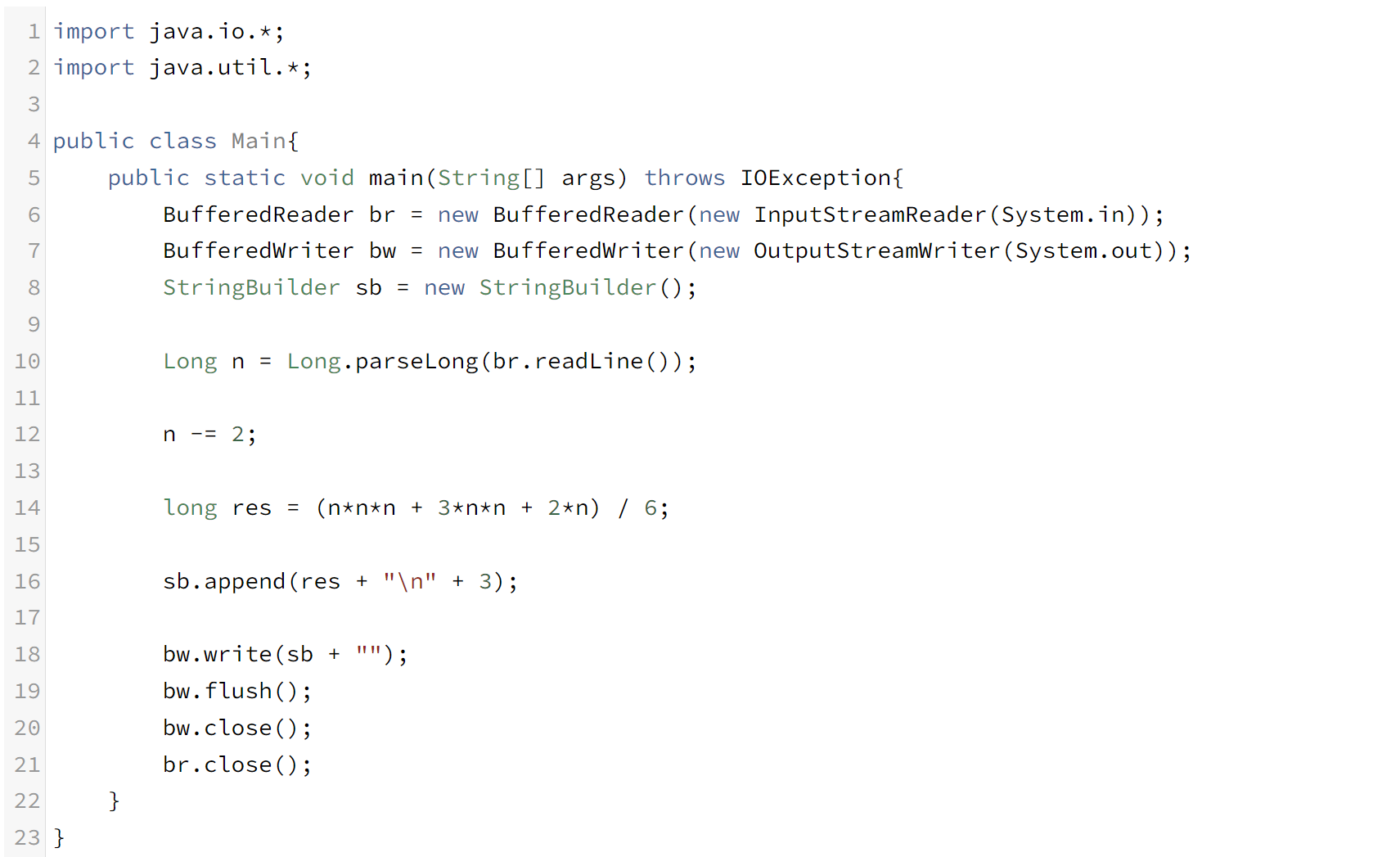
an = 1/6 * ( n³ + 3n² + 2n )
이라는 공식이 나온다
n은 3부터 시작되었으니 n -= 2; 를해주고 계산을 해야한다.